Planetary-Scale Inference: Previewing our Peer-To-Peer Decentralized Inference Stack

We are excited to share a preview of our peer-to-peer decentralized inference stack — engineered for consumer GPUs and the 100ms latencies of the public internet—plus a research roadmap that scales it into a planetary-scale inference engine.

At Prime Intellect, we’re building towards an open and decentralized AGI future—one where anyone with consumer-grade hardware and a network connection can meaningfully contribute to and benefit from AGI. This means designing for the real world: heterogeneous GPUs, public internet latency, and unreliable but abundant FLOPs. With the rise of reinforcement learning for reasoning models like DeepSeek R1, inference has moved to center stage, and is now a core component of the entire AI stack:

• Training: Generate rollouts during reinforcement learning (e.g. INTELLECT-2)
• Distillation: Creating synthetic data at scale (e.g. SYNTHETIC-1)
• Evaluation: Benchmarking model performance and safety

That’s why our next step is decentralizing inference itself.

Designing for High-Latency Networks

However, decentralizing inference is a non-trivial problem, as it is heavily constrained by network communication. In the remainder of the blog post, we go into technical detail of why this is and share ideas on how to circumvent key bottlenecks that we identify. Here is the TL;DR:

• Because of its low communication requirements, pipeline parallelism is best suited for decentralized environments.
• However, naive pipeline parallelism suffers from GPU idle time caused by sequential processing.
• Surprisingly, asynchronous micro-batch pipeline schedules (like ZeroBubble) are effective for compute-bound workloads like training but not for inference workloads, which are typically bounded by memory bandwidth and total memory
  • When not compute-bound, processing one or two sequences takes roughly the same time — we gain "free" throughput by parallel decoding.
  • The KV cache's high memory demands grow with parallel sequence decoding, preventing compute-bound operation (which would occur at $B_{crit}$). Thus, we stay in the "~linear throughput scaling" regime until reaching maximum batch size $B_{max}\ll B_{crit}$.
  • Consider $N$ devices running either a synchronous schedule with $B_{max}$ or an asynchronous schedule with $N$ micro-batches of size $B_{max}/N$: Due to linear throughput scaling, processing either the full batch or a micro-batch takes time $T$. The total time is $NT$ whether a device processes all micro-batches or processes the full batch and waits $(N-1)\cdot T$ for pipeline completion.
  • Increasing the number of pipeline stages doesn't improve throughput because doubling the stages only doubles the maximum batch size — if $B_{max}$ sequences fit on $N$ devices, then $2B_{max}$ fit on $2N$ devices. For pipelines with $N$ and $2N$ devices, the micro-batch sizes are equivalent ($B_{max}/N=$ $2B_{max}/2N$), yielding no throughput gains.
• This makes synchronous pipeline schedules, as implemented in vLLM, a strong baseline.
• Achieving higher throughput in high-latency environments requires reimagining the inference process. The key will be converting memory requirements into compute requirements—a viable approach in decentralized settings where network-induced idle time can be used for asynchronous computation.

Today's Releases

Alongside the blog post, we are open-sourcing three research codebases that build towards latency-aware pipeline parallelism:

1. PRIME-IROH: A peer-to-peer communication backend designed for pipeline parallel communication
2. PRIME-VLLM: A pipeline-parallel vLLM integration that runs over public networks
3. PRIME-PIPELINE: A minimal research sandbox for quickly validating research ideas, such as novel cache mechanisms and pipeline schedules

With today's releases you can already connect private hardware to run inference over public networks. We are actively working on integrating these components into our own stack, like our Protocol testnet and TOPLOC verification scheme, to enable our largest public synthetic data run, SYNTHETIC-2.

Traditional Inference

In this section, we introduce mathematical notation to reason about the runtime of operations on GPUs to analyze bottlenecking factors during inference workloads on a single node. Much of the notation is borrowed from How To Scale Your Model by Google DeepMind.

If you are already familiar with traditional inference math, skip to Decentralized Inference.

Accelerator Math

Whenever we run an operation on an accelerator, there are two things that take time:

Computation: How long it takes to compute all the floating-point operations (FLOPs) required for the operation

$$T_{\text{comp}}=\frac{\text{Compute Volume [FLOPs]}}{\text{Compute Speed [FLOPs/s]}}$$

Communication: How long it takes to move all bytes required for the operation from an external device to the compute cores of the accelerator

$$T_{\text{comm}}=\text{Communication Latency}+\frac{\text{Communication Volume [Bytes]}}{\text{Communication Bandwidth [Bytes/s]}}$$

Depending on the communication workload, $T_{\text{comm}}$ is typically dominated by one of the two terms, i.e., it is well approximated by either the latency or bandwidth term. Further, communication happens through all stages of the memory and network hierarchy, but in general we focus on two types of communication.

On-Chip Communication: Data transfers between on-chip memory and compute cores

$$T_{\text{mem}}=\text{Memory Latency}+\frac{\text{Communication Volume [Bytes]}}{\text{Memory Bandwidth [Bytes/s]}}$$

Note that on-chip memory moves for inference workloads are highly bandwidth-bound, so this term is well approximated by the bandwidth term.

$$T_{\text{mem}}\approxeq \frac{\text{Communication Volume [Bytes]}}{\text{Memory Bandwidth [Bytes/s]}}$$

Network Communication: Data transfers between multiple hosts

$$T_{\text{net}}=\text{Network Latency}+\frac{\text{Communication Volume [Bytes]}}{\text{Network Bandwidth [Bytes/s]}}$$

Depending on the communication requirements of the operation, this term may be dominated by either latency and/or bandwidth. We will revisit it in the section Decentralized Inference.

Roofline Analysis

How does compute and communication interact? In the worst case, computation and data transfer cannot be overlapped, and so the total time for an operation to complete is the time it takes for each part to complete, i.e.

$$T=T_{\text{comp}}+T_{\text{mem}}+T_{\text{net}}$$

In the best case, all computation and communication can be overlapped, and so the total time for the operation to complete is equivalent to the part that takes the longest, i.e.

$$T=\max(T_{\text{comp}},T_{\text{mem}},T_{\text{net}})$$

For the rest of our discussion, we'll use this latter notation of taking the maximum time. This allows us to identify different performance regimes based on which factor becomes the bottleneck - this type of analysis is called roofline analysis:

• Compute-Bound ($T_{\text{comp}}>T_{\text{mem}},T_{\text{net}}$): Most time is spent computing - memory and network sit idle
• Memory Bandwidth-Bound ($T_{\text{mem}}>T_{\text{comp}}, T_{\text{net}}$): Most time is spent moving data to and from memory - compute and network sit idle
• Network-Bound ($T_{\text{net}}>T_{\text{comp}}, T_{\text{mem}}$): Most time is spent waiting for the network - compute and memory sit idle

Generally, we always want to be compute-bound. If not, we are wasting FLOPs, which often equates to wasting money.

Operation vs. Accelerator Intensity

For operations running on a single accelerator (no network communication), a good way to tell if an operation is likely compute or memory-bandwidth bound is to look at its FLOPS per byte, sometimes called the operation intensity, defined as

$$\text{Intensity(OP)}=\frac{\text{Computation Volume [FLOPs]}}{\text{Communication Volume [Bytes]}}$$

It’s useful to think of this as the amount of computation done per memory move. Intuitively, if this ratio is high, we are likely compute-bound, else memory bandwidth-bound. We can quantify precisely in which regime we are by comparing to the accelerator intensity, defined as

$$\text{Intensity}(\textsf{Accelerator})=\frac{\text{Compute Speed [FLOPs/s]}}{\text{Memory Bandwidth [Bytes/s]}}$$

This constant is the peak FLOPs per byte that we can expect from our hardware. For example, for a H100 the accelerator intensity is $989e^{12} / 3.35e^{12} \approx 295$ (GitHub Gist). By simple re-arrangement we get that we are in the compute-bound regime for operation intensities that exceed our accelerator intensity.

$$\begin{align*}T_{\text{comp}}>T_{\text{mem}}&\iff \frac{\text{Compute Volume [FLOPs]}}{\text{Compute Speed [FLOPs/s]}}>\frac{\text{Communication Volume [Bytes]}}{\text{Memory Bandwidth [Bytes/s]}} \\&\iff \frac{\text{Compute Volume [FLOPs]}}{\text{Communication Volume [Bytes]}}>\frac{\text{Compute Speed [FLOPs/s]}}{\text{Memory Bandwidth [Bytes/s]}} \\&\iff \text{Intensity(OP)} > \text{Intensity(Accelerator)}\end{align*}$$

Example: Dot Product

Let’s look at a simple example: Consider the dot product ($\circ$) between two $n$-dimensional vectors $u, v\in \mathbb{R}^{n}$ defined as $u\circ v=\sum_i u_i v_i$. We have the following tensor signature:

$$\textsf{DotProduct}= \text{bf16}[N], \text{bf16}[N]\rightarrow \text{bf16}[1]$$

How many FLOPs do we need to compute and bytes do we need to move? Let’s count:

• Load both vectors (Total Bytes: $2N+2N$)
• Compute element-wise products (Total FLOPs: $N$ multiplications)
• Compute the sum of all elements (Total FLOPs: $N-1$ additions)
• Save the scalar result (Total Bytes: $2$)

Counting up all the FLOPs and all the bytes, we get the following operation intensity as $N\rightarrow\infty$

$$\text{Intensity}(\textsf{DotProduct})=\frac{N+N-1}{2N+2N+2}=\frac{2N-1}{4N+2}\rightarrow\frac{2N}{4N}=\frac{1}{2}$$

We only do half a FLOP per byte moved. This is pretty bad - we do more byte loads than FLOPs for each dot product, but GPUs are designed for massive parallel processing. Since, $1/2<\text{Intensity}(\textrm{Accelerator})$ for almost all accelerators, dot products are notoriously memory bandwidth-bound (GitHub Gist).

Inference Process

Naive Sampling

All frontier models generate text auto-regressively: The model processes a context of tokens to obtain a probability distribution over all possible next tokens. It then samples from this distribution, appends the new token, and repeats the process. Naively implemented, the entire context is passed at every decoding step. Generating n tokens is a $\mathcal{O}(n^2)$ operation for the feed-forward block and $\mathcal{O}(n^3)$ operation for self-attention block. Such order-of-growth is prohibitive for most practical contexts (read: long generations).

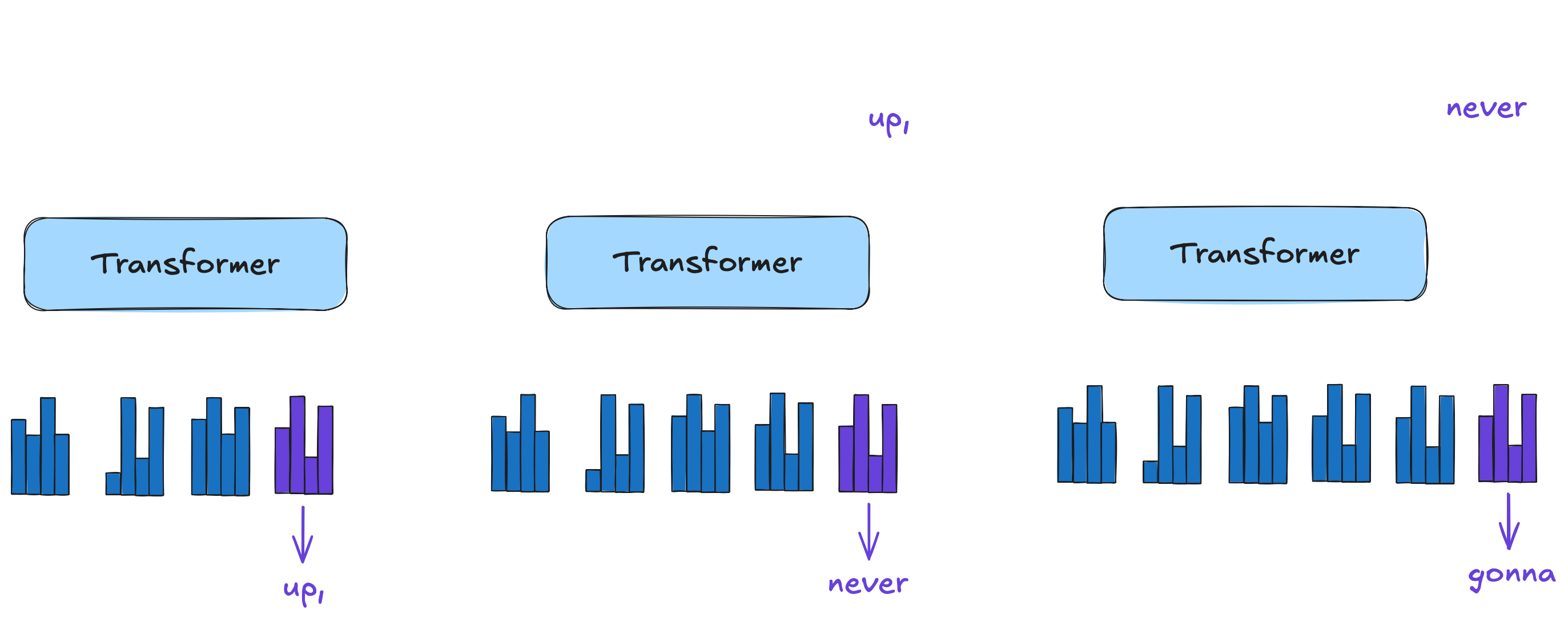
Sampling with KV Cache

To address this, it is standard practice to use a KV cache: instead of recomputing keys and values for all context tokens at each step, we store them in memory. This works efficiently because at each decode step, we only need to compute two dot products: one between the current token's query vector and the past keys, and another between the current token's attention vector and the past values. By avoiding the costly recomputation of keys and values for past tokens, we reduce the order-of-growth by a linear factor to $\mathcal{O}(n)$ for the feed-forward and $\mathcal{O}(n^2)$ for the attention block.

‍

With caching, the inference phase can be split into two distinct phases:

1. Prefill: Given a prompt, we populate the KV cache and decode the next token‍
2. Decode: Given the KV cache and previous token, update the cache and decode the next token

As we will see, these two operations are vastly different in terms of their computational needs. To see this, we analyze the operation intensities of one prefill and decode step.

‍Inference Intensity

Pre-filling and decoding are forward passes through the model, involving token embedding, positional encoding, self-attention blocks, feed-forward networks, and a language model head. We can focus primarily on matrix multiplications in linear layers since they account for most FLOPs. During training, modeling these matrix multiplications provides accurate estimates for a training step time. For (long-context) inference, we must also consider the self-attention block because of heavy memory moves due to the KV cache. This leaves two main operations to focus on:

• Linear layers: We spend the vast majority of FLOPs on matrix multiplications between activations and weight matrices: In the MLP block there are huge matrices $W_{in}$, $W_{out}$ (sometimes also $W_{gate}$), and in the self-attention block we have the projection matrices  $W_Q$, $W_K$, $W_V$, $W_O$.
• Self-Attention: Given the current query, key and value vectors $Q$, $K$ and $V$, we compute an attention matrix $A=QK^T$ and output $AV$, with an interleaved softmax, and masking operation. This operation requires all past keys and values, stored in the potentially large $K$ and $V$ matrices.

Getting an idea of whether we are compute or memory bandwidth-bound in these two operations will allow us to lower bound the time it takes for one prefill and decode step.

Linear Layers

All linear layers are matrix multiplications $XW$ between activations $X\in\mathbb{R}^{B\times T\times D}$ and weights $W\in\mathbb{R}^{D\times F}$. In a forward pass, we typically have the following tensor signature:

$$\textsf{MatMul}: \text{bf16}[B, T, D], \text{bf16}[D,F] \rightarrow \text{bf16}[B,T,F]$$

Like with the dot product, let’s check the FLOPs and memory moves required:

• Load both input matrices (Total Bytes: $2BTD+2DF$)
• Compute matrix product (Total FLOPs: $2BTDF$)
• Save the output matrix (Total Bytes: $2BTF$)

This gives us the following operation intensity of a matrix multiplication:

$$\text{Intensity(MatMul)=}\frac{2BTDF}{2BTD+2DF+2BTF}\approxeq_{BT\ll D,F} \frac{BTDF}{DF}=BT$$

We get a nice simplification of the denominator under the assumption that the total number of batched tokens (product of the batch and sequence dimension) is very small in comparison to the input and output dimension (which is reasonable for Transformers). The operation intensity scales with the number of tokens that are being processed in parallel, i.e., the larger $BT$, the higher the compute density (GitHub Gist). This can be intuited by the fact that the cost of matrix multiplication scales as $\mathcal{O}(n^3)$, while the memory cost only scales as $\mathcal{O}(n^2)$. Recall that we have $T_{\text{comp}}>T_{\text{mem}} \iff \text{Intensity(MatMul)} > \text{Intensity(Accelerator))}$. Assuming an H100, this means that as long as $BT>295:=B_{\text{crit}}$, we are in our happy zone and compute-bound. Now, how likely are we to get into this regime during our two phases in inference?

• Prefill: We process multiple tokens, possibly even multiple sequences, in parallel. Even if $B=1$, it is quite realistic that we already have $T>B_{crit}$ if simply the number of prompt tokens exceeds the critical batch size.
• Decode: We cannot process multiple tokens in the same sequence in parallel because of auto-regressiveness, i.e., $T=1$. This means our only way of parallel processing is across the batch dimension. We need $B>B_{crit}$ to be in the compute-bound regime.

Self-Attention

In self-attention, we compute attention scores between $T$ query tokens and $S$ key-value tokens and produce an output given by $\text{softmax}(QK^T/{\sqrt{D}})V$. Typically, we have multiple attention heads, but we focus on a single head for simplicity. The tensor signature is given by

$$\textsf{Attention}: \text{bf16}[B, T, D], \text{bf16}[B,S,D], \text{bf16}[B,S,D] , \rightarrow \text{bf16}[B,T,D]$$

Let's count FLOPs and bytes for a single head. We will omit element-wise operations, like the scaling factor and softmax, which are negligible and often fused into other operations.

• Read the $Q$ activations (Total Bytes: $2BTD$)
• Read the $KV$ cache (Total Bytes: $2BSD + 2BSD$)
• Compute $A=QK^T$ (FLOPs: $2BSTD$)
• Compute $AV$ (FLOPs: $2BSTD$)
• Save the result (Total Bytes: $2BTD$)

Putting this together, we get the following operation intensity:

$$\text{Intensity(Attention)}=\frac{4BSTD}{4BSD+4BTD}=\frac{ST}{S+T}$$

The FLOPs to bytes ratio depends on the ratio of key to query tokens $S$ and $T$ — the ratio of key-value to query tokens:

• Prefill: During prefill, we perform regular self-attention, i.e., $S=T$. Substituting in, we get $T^2/2T=T/2=\mathcal{O}(T)$. This means that as long as the number of prompt tokens is proportional to our critical batch size $\mathcal{O}(T)>B_{crit}$, we are compute-bound.
• Decoding: During decoding, we have $T=1$, which plays out like this: $S\gg T=1\implies ST/S+T\approx 1$. We are fundamentally memory bandwidth-bound (!). No matter how many sequences we are batching together in parallel, we always spend the majority of time moving the heavy KV cache

Memory Capacity

During decoding, we are memory-bandwidth bound. We can move closer to the compute-bound regime for matrix multiplications by increasing the number of sequences decoded in parallel. However, unlike in training, memory pressure grows with larger batches because each sequence in a batch has a unique KV cache. Let’s compute the maximum batch size that we can fit.

Model weights: We have to store each parameter in the model. Assuming half precision, we get:

$$\text{Model Size}:= 2\cdot P$$

KV cache: Assuming regular multi-head attention (MHA), we have to store $H$-dimensional keys and values across all $L$  layers and $K$ key-value heads for each token. Again, assuming half precision, we get:

$$\text{KV Cache Size} := 2\cdot 2\cdot H\cdot K\cdot L$$

Let’s check what this means for LLama-2 13B. The memory for weights is trivial - we have $P=13B$ and so we need roughly $26\text{ GB}$ for storing the weights. What about the KV cache? The model uses regular MHA and has $H=128$, $K=40$ and $L=40$. Plugging in, we get:

$$2\cdot2 \cdot 128 (H) \cdot 40 (K)\cdot 40 (L)\approx 0.82 \text{ MB}$$

We need almost one megabyte for every token that we cache! If we assume that we generate sequences of length $4096$ (the maximum context of the model), we need $3.35\text{ GB}$ for each sequence that we decode. This is bad news! We would like to decode many sequences in parallel (large $B$) to make better use of our FLOPs but our maximum batch size $B_{max}$ is limited by the KV cache. For some constant $C$  reserved for intermediate activations, we get:

$$B_{max}:=\left\lfloor\frac{\text{Accelerator Memory}-\text{Model Size}-C}{T\cdot \text{KV Cache Size}}\right\rfloor$$

Let’s check the maximum batch sizes for each model in the Llama-2 series for different accelerator memory capacities (GitHub Gist).

No single GPU can serve the 70B model (without quantization) because just storing the weights requires 140GB of accelerator memory. All GPUs can run the 7B model, but even for the smallest model we are nowhere near the critical batch size required to be compute-bound on modern accelerators, i.e. $B_{max}\ll B_{crit}$. Thus, we are fundamentally memory bandwidth-bound during auto-regressive decoding.

This precise finding has put a lot of optimization pressure on improving the memory usage of LLMs during inference, which has led to many innovations, such as MQA, GQA, MLA, Sliding Window Attention, Paged Attention, and many more. We will not cover these in detail here, but consider traditional (unoptimized) architectures using multi-head attention (MHA).

Inference Throughput

Given these findings, how can we get an approximate final inference performance? For the type of workload that we are interested in — synthetic data generation, reinforcement learning rollouts and evals — we have a large batch of "requests" available at all times and wish to optimize for the total token throughput, typically measured in tokens per second. How can we upper bound this property? With each prefill or decoding step, we are generating one new token for each sequence in the batch. Thus, we are generating $B$ tokens in the time it takes for a prefill or decode step, i.e

$$\text{Throughput}=\frac{B}{\text{Step Time}}$$

By obtaining a lower bound on the step time we can upper bound throughput. We have already  worked towards lower bounding this property in the previous section. Recall, that the time for a single decode step is dominated by the time spent on matrix multiplications and during self-attention, i.e.

$$\text{Decode Time}\approxeq T(\textsf{Linear})+T(\textsf{Attention})$$

Further, because $T\geq 1\implies BT\geq B$ we always have

$$\text{Prefill Time} \geq \text{Decode Time}$$

And so we can lower bound the step time as

$$\text{Step Time}\geq \text{Decode Time}\approxeq T(\textsf{Linear})+T(\textsf{Attention})$$

As we have seen, $T(\textsf{Linear})$ may be compute-bound or memory-bandwidth bound during decode, depending on the batch size $B$ used. Therefore, we have

$$T(\textsf{Linear})=\max(T_{\text{comp}}(\textsf{Linear}), T_{\text{mem}}(\textsf{Linear}))$$

How many FLOPs and bytes do we spend on matrix multiplications for a full forward pass? A handy rule of thumb is that we roughly do $2BP$ FLOPs and $2P$ byte moves (for a thorough analysis, see Transformer Inference Arithmetic). Given this, we get pretty simple formulas:

$$T_{\text{comp}}(\textsf{Linear})=\frac{2BP}{\text{Compute Speed [FLOPs/s]}}$$

$$T_{\text{mem}}(\textsf{Linear})=\frac{2P}{\text{Memory Bandwidth [Bytes/s]}}$$

Approximating $T(\textsf{Attention})$ is even easier because we have already shown that this operation is fundamentally bandwidth-bound during decoding and dominated by the cost to move the KV cache. To decode a token at step $t=1,\dots,T$, we need to load $t-1$ past keys and values. Therefore, we can approximate the average time for generating $T$ tokens as:

$$T_{\text{mem}}(\textsf{Attention})=\frac{B\cdot T\cdot \text{KV Cache Size}}{2 \cdot \text{Memory Bandwidth [Bytes/s]}}$$

Putting all of these formulas together, we can lower bound the step time and, consequently, upper bound throughput. Below we are showing the peak theoretical throughput as a function of batch size (up to the maximum batch size that can be fit) for different models running on different GPUs.

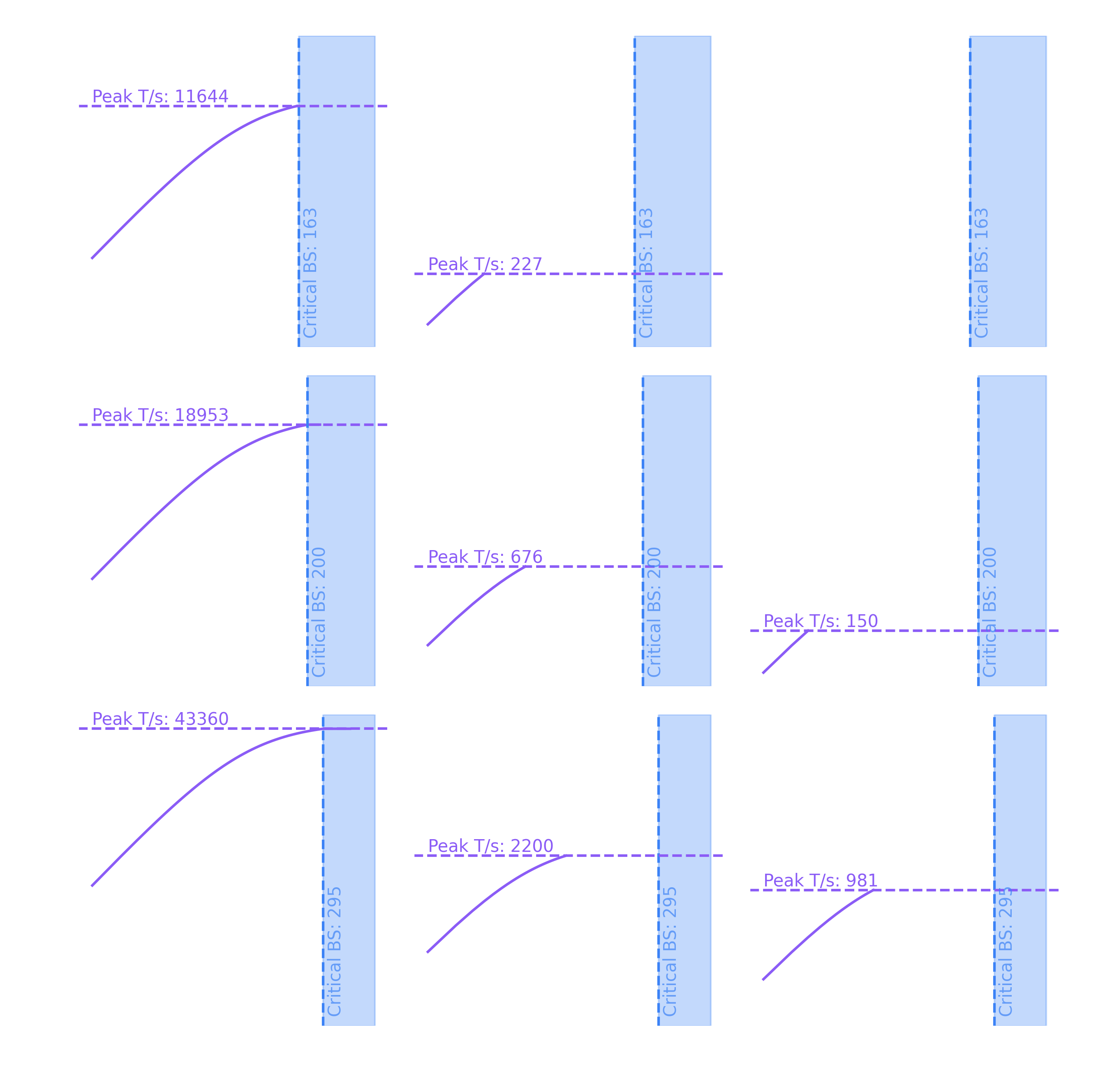
The plot reveals several key insights:

• Since we are fundamentally memory bandwidth-bound (from moving parameters and KV cache), we achieve nearly linear throughput scaling. Doubling the batch size almost doubles the throughput, with only slight diminishing returns due to the proportionally growing KV cache.
• Once we reach the compute-bound threshold, increasing the batch size yields no additional throughput gains.
• Yet even small models like Llama-2 7B using traditional MHA never reach the critical batch size needed to become compute-bound. Instead, they remain in the "linear throughput scale" regime until hitting the accelerator's maximum batch size limit.

Decentralized Inference

Frontier models rarely fit on a single accelerator, and so it is imperative to shard the model itself to reduce the memory requirements per-device. There are mainly two types of model parallelism:

Tensor Parallelism (TP) shards weight matrices; computes and communicates partial results

Pipeline Parallelism (PP) shards layers; computes layers sequentially and communicates intermediate activations/generated tokens

Depending on the type of parallelism, there are different network synchronization points during a forward pass, and so the network communication contributes to the step time differently. Assuming $N$-way parallelism, the number of communication synchronization points during a single forward pass scales as $\mathcal{O}(NL)$ in TP, and $\mathcal{O}(N)$ in PP. The additional factor $\mathcal{O}(L)$ in TP stems from the fact that it requires communication within each layer to accumulate partial results of sharded matrices. In decentralized settings, we have to opt for the parallelism technique with the smallest communication requirements. This leaves pipeline parallelism as the only viable option for running extremely large models on consumer hardware over public networks. Let's understand pipeline parallelism in detail.

Pipeline Parallelism

In PP, each device handles a contiguous sequences of layers, called a model shard. Assuming $N$ devices, this intuitively means that each device now handles $1/N$ of the model.

One of the main advantages of pipeline parallelism is that the memory decreases proportional to the degree of parallelism $N$. Enumerating devices as $i=1,\dots,N$, we get

$$\text{Local Model Size}_i\approxeq\frac{\text{Model Size}}{N},\quad\text{Local KV Cache Size}_i=\frac{\text{KV Cache Size}}{N}$$

The memory required to store the shard's parameters and cache decreases! This enables running models of arbitrary size on arbitrary hardware. For example, we can run Llama-2 70B on 2×H100s with $2\cdot 80=180\text{ GB}$, 4×A100s with $4\cdot 40GB=160\text{ GB}$, or 8×4090s with $8\cdot 24=192\text{ GB}$ unified memory. However, sharding the model layer-wise introduces communication synchronization points. Nodes are arranged sequentially and have to communicate intermediate results with adjacent pipeline stages. Because of auto-regressive generation, the last stage device has to send the next generated token back to the first stage device before the subsequent decoding step, leading to a ring network topology.

Synchronous Pipelining

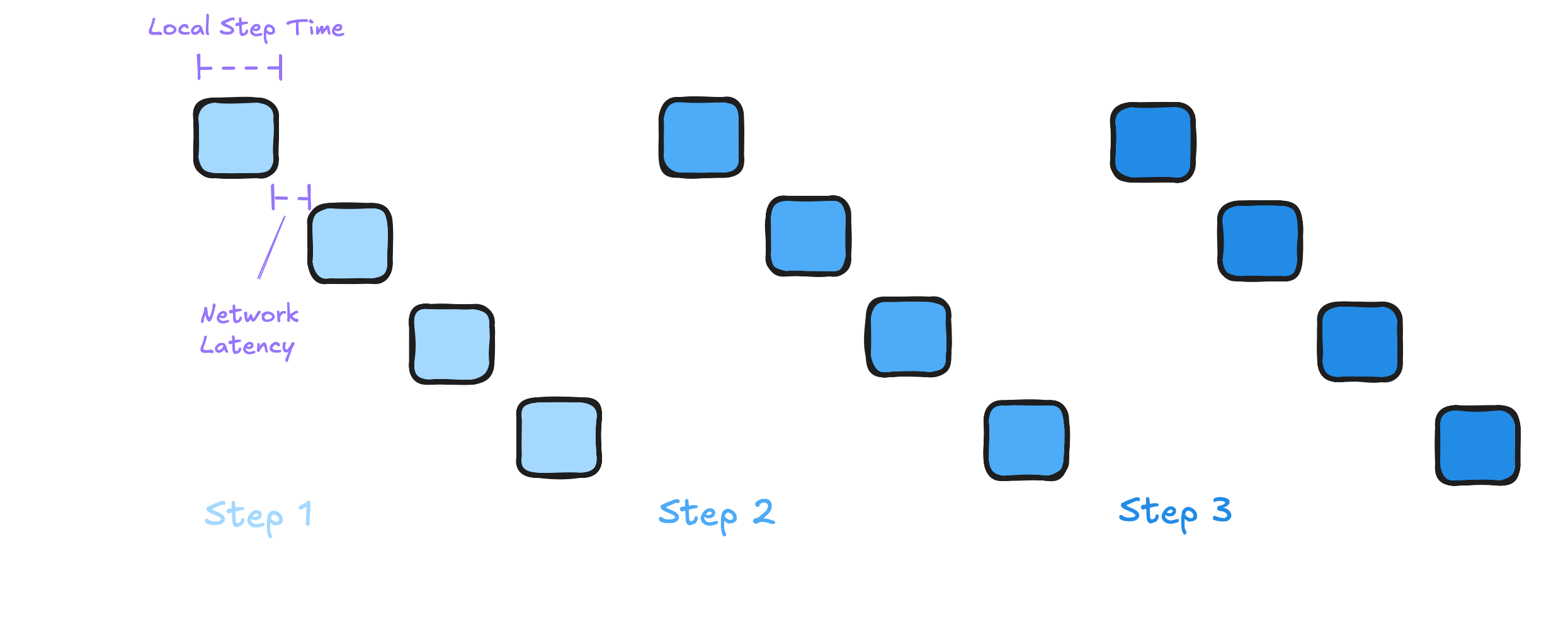
One of the simplest pipeline schedules is a synchronous blocking schedule, where each device waits for the remaining pipeline workers to complete their work.

There is a strict sequential dependency in this process. At any point in time, only one of the $N$ workers is working while all others sit idle! How does the step time compare to a single device? Recall that on single accelerators, we lower-bounded the step time as $\text{Step Time}\geq T(\textsf{Linear})+T(\textsf{Attention})$. For $N$-way pipeline parallelism, both $T(\textsf{Linear})$ and $T(\textsf{Attention})$ scale with the number of layers $L$, and are therefore reduced by a factor $N$ when pipelining. Thus, we also get a factor $N$ reduction in the per-device step time.

$$\text{Local Step Time}_i=\frac{\text{Step Time}}{N}$$

But due to sequential processing, the overall step time is the sum of all local steps, and so we find that the step time is $N\cdot \text{Local Step Time}_i=\text{Step Time}$. This implies that we cannot hope for higher throughput for a fixed batch size as we increase the degree of parallelism. In fact, we cannot even hope to do as well as the single-device step time because of network overhead. The per-step network overhead in synchronous schedule can be approximated as the sum of latencies between each pipeline stage:

$$T_{\text{net}}\approxeq  N\cdot \text{Network Latency}$$

Note that we make the simplifying assumption that the network cost is dominated by the latency as opposed to bandwidth. Because we assume blocking send and receive operations, the communication cost is additive, and we get the following true step time.

$$\text{Step Time}_{PP}=N\cdot \text{Network Latency} + \text{Step Time}$$

Let's assume a common cross-continental latency of 100ms. Even if we completely ignore the per-device processing time, the peak theoretical throughput is bound by network latency.

$$\text{Throughput/PP} = \frac{B}{\text{Step Time/PP}} \leq \frac{B}{N \cdot \text{Network Latency}}$$

To see just how much we are bottlenecked, let's check the maximal theoretical throughput for a $N=2$ pipeline for a single-batch generation.

$$\frac{1}{2\cdot (100/1000)} \approx 5\text{ tokens/s}$$

The network overhead puts a hard ceiling on the maximum throughput we can hope for! No optimization which improves the on-device compute and memory transfer time will be able to break this ceiling (we already assumed zero on-device time). Recall that on an H100 we got a theoretical upper bound of 121 tokens/s for single-sequence throughput of Llama-2 13B.

Trading-Off Memory and Latency

However, we are most interested in increasing peak throughput, which occurs when decoding $B_{max}$  sequences in parallel. Because pipeline parallelism reduces the total memory footprint by a factor $N$, we can scale $B_{max}$  by at least the same factor. Thus, with every doubling of our pipeline, we can (at least) double the maximum batch size. At the same time, scaling the pipeline size introduces more network communication, further increasing latency. Is this trade-off worth it?

$$
\begin{align*}
\text{Throughput}_{PP} &> \text{Throughput} \\
\iff & \frac{NB_{max}}{N \cdot \text{Latency} + \text{Step Time}} > \frac{B_{max}}{\text{Step Time}} \\
\iff & NB_{max} \cdot \text{Step Time} > B_{max} \cdot (N \cdot \text{Latency} + \text{Step Time}) \\
\iff & N \cdot \text{Step Time} > N \cdot \text{Latency} + \text{Step Time} \\
\iff & (N-1) \cdot \text{Step Time} > N \cdot \text{Latency} \\
\implies & \text{Step Time} > \text{Latency} \quad (\text{approx. for large } N)
\end{align*}
$$

Scaling the pipeline only improves peak throughput if the step time is larger than the latency. However, when running over public networks, the expected latency is often higher than the step time (often <20ms).

Asynchronous Pipelining

The sequential nature of data flow through pipelines is its main disadvantage: if naively implemented, it incurs significant device idle time. For training workloads, there exists a lot of literature that tries to increase the level of parallelism by overlapping micro-batched forward and backward passes through advanced pipeline schedules.

Can we use a similar idea for inference? Assuming $N$ devices and no latency, the following algorithm is natural:

• Split the total batch size $B$ into $N$ micro batches (each of micro-batch size $B/N$)
• For each device: Process and asynchronously send/receive micro-batches

For $N=4$, such an asynchronous micro-batch pipeline schedule would look like this.

While there is some unavoidable pipeline bubble at the beginning and the end of the inference process, this overhead is constant and amortizes for long generations. Can we hope for the same strong scaling of throughput as during training? Unfortunately, for as long as we are memory bandwidth-bound, instead of compute-bound (which we are during decoding), we have that the time to process a micro-batch is roughly the same as the time to process a full batch, let's denote this as time $T$. The total time is $NT$ whether a device processes all micro-batches or processes the full batch and waits $(N-1)\cdot T$ for pipeline completion.

Synchronous batched schedule. Schedule for 4 devices with a single full (original four micro-batched), unrolled over 4 decoding steps, assuming no latency. At each step, each device synchronously receives, processes and sends intermediate micro-batch results, resulting in idle time.

We need the same time for a single step: either we process the full batch and wait, or process all micro-batches in parallel. Thus, we are trading increased parallelism for reduced per-step throughput and gain nothing. This is because we are memory-bandwidth bound, so increasing the batch size yields "free" throughput gains because the operation time is dominated by moving parameters, not the actual computation.

Research Roadmap

We will use our findings and learnings to work towards a decentralized inference engine designed for real-world networks with high latency and heterogeneous hardware. Achieving higher throughput in such environments will require reimagining accepted truths in inference optimization. Our research will focus on:

1. Increasing Compute Density: Exploring ways to better utilize idle compute time during network waits by shifting memory-bound operations toward compute-heavy execution
2. Reducing Memory Footprint: Investigating techniques to minimize memory requirements during decoding, including lighter cache management and strategic re-computation
3. Enabling Asynchronous Execution: Designing naturally asynchronous inference protocols that can tolerate variability in node availability, latency, and bandwidth without sacrificing throughput

References

• https://kipp.ly/transformer-inference-arithmetic/
• https://jax-ml.github.io/scaling-book/
• https://fleetwood.dev/posts/domain-specific-architectures
• https://horace.io/brrr_intro.html
• https://arxiv.org/abs/2309.06180