INTELLECT-3: A 100B+ MoE trained with large-scale RL

Today, we release INTELLECT-3, a 100B+ parameter Mixture-of-Experts model trained on our RL stack, achieving state-of-the-art performance for its size across math, code, science and reasoning benchmarks, outperforming many larger frontier models.

Our complete recipe — from the model weights and training frameworks, to our datasets, RL environments, and evaluations — has been open-sourced, with the goal of encouraging more open research on large scale reinforcement learning.

INTELLECT-3 is trained on the same software and infrastructure that we’re open-sourcing and making available on our platform at Prime Intellect, giving everyone the tools to post-train their own state-of-the-art models, and moving us towards a future where every company can be an AI company.

Chat with INTELLECT-3 at chat.primeintellect.ai

Benchmarks

INTELLECT-3 is a 106B parameter Mixture-of-Experts model trained with both SFT and RL on top of the GLM 4.5 Air base model. It achieves state-of-the-art performance for its size across math, code, science and reasoning benchmarks.

Training Infrastructure

We leverage the following infrastructure components for training:

• PRIME-RL: Our custom asynchronous RL framework powering both supervised fine-tuning and large-scale reinforcement learning of Mixture-of-Experts models.
• Verifiers and the Environments Hub: A unified environment interface and ecosystem foragentic RL training environments and evaluations.
• Prime Sandboxes: High-throughput, secure code execution for agentic coding environ-ments.
• Compute Orchestration: Orchestrated and managed 512 NVIDIA H200 GPUs across 64 interconnected nodes.

PRIME-RL

INTELLECT-3 was trained end-to-end with prime-rl, our production-scale post-training frame-work. prime-rl provides native integration with verifiers environments, which power our entire post-training stack from synthetic data generation, supervised fine-tuning, reinforcement learning, to evaluations. Through its tight connection to the Environments Hub, the entire training stack can seamlessly access a rapidly expanding ecosystem of training and eval environments.

The sharpest distinction between prime-rl and many other RL trainers is that it is async-only — we recognized fairly early (for our previous INTELLECT-2 model) that the future of RL is async; i.e. always a few steps off-policy. Async training is simply the only practical way to efficiently scale RL to long-horizon agentic rollouts without incurring bottlenecks based on the slowest rollouts per step.

Over the past six months we’ve focused heavily on ablations for performance, stability, and efficiency at scale. INTELLECT-3 is a culmination of our work, scaling RL to train a 100B+ parameter Mixture-of-Experts model on 512 NVIDIA H200 GPUs. For more details on how our trainer works, see our technical report.

We will soon be releasing a hosted entrypoint to prime-rl as part of our upcoming Lab platform, enabling large-scale RL training without the infrastructure overhead.

Verifiers & Environments Hub

We train INTELLECT-3 using environments built with our verifiers library and hosted on the Environments Hub, our community hub for RL environments and evaluations.

verifiers is the leading open-source toolkit for creating RL environments and evaluations for LLMs. It provides a set of modular and extensible components for concisely expressing complex environment logic while maintaining highly scalable performance.

Most RL frameworks tightly couple environments into the training repo, making versioning, ablations, and external contributions cumbersome. The Environments Hub decouples this by publishing verifier-backed environments as standalone, pinnable Python modules with a uniform entry point. This allows tasks to be versioned, shared, and iterated on independently.

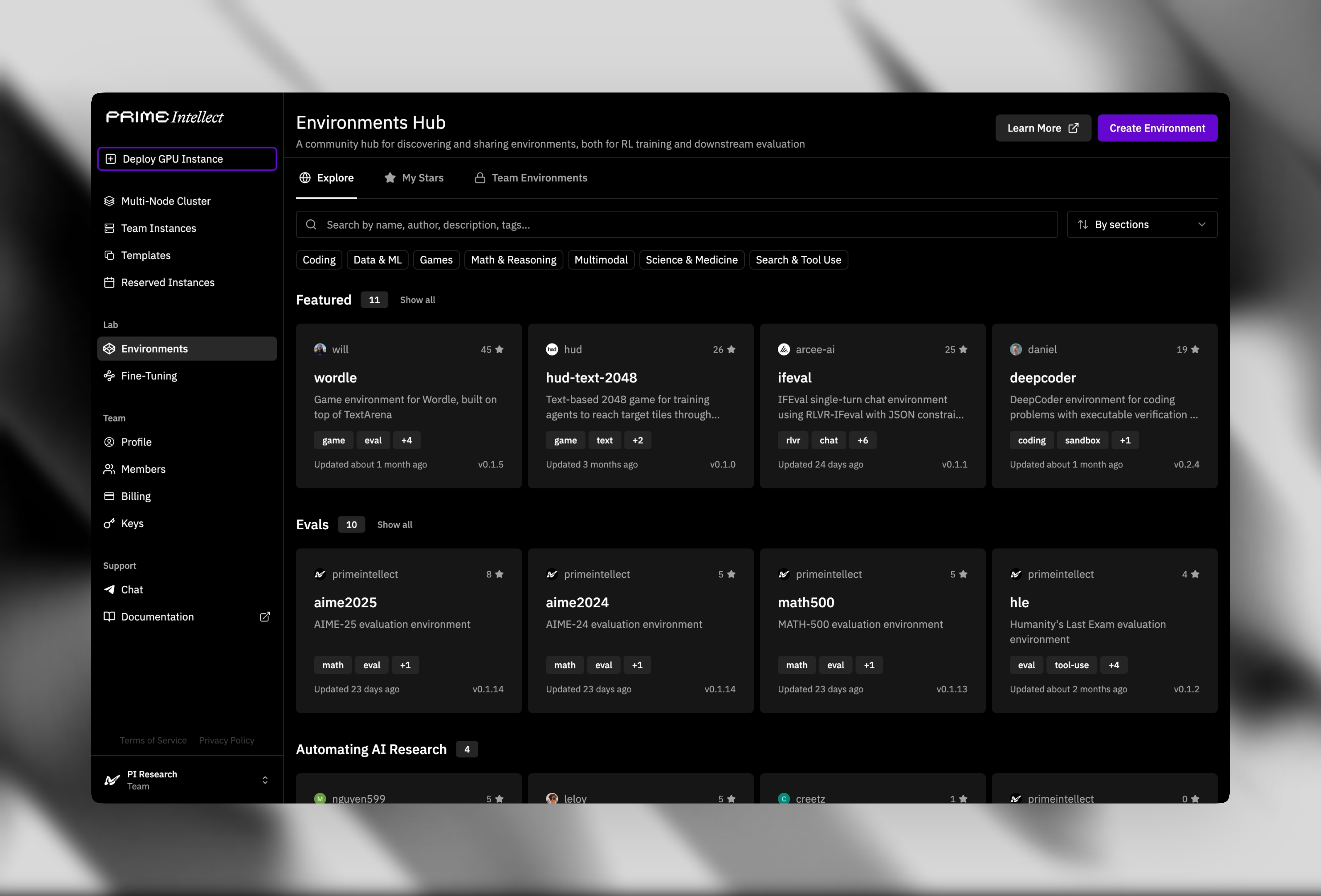
All the environments and evaluations used for INTELLECT-3 are publicly available for others to use on the Environments Hub. For more details on the specific environments, as well as how they integrate with our trainer, see our technical report.

Prime Sandboxes

We scaled and upgraded our custom Sandboxes infrastructure specifically for agentic RL.

Executing untrusted code for thousands of concurrent rollouts requires a container orchestration layer capable of sub-second provisioning and millisecond-level execution latency. While Kubernetes provides the primitives for container management, standard architectural patterns are insufficient for the throughput required by high-velocity training.

To overcome these limitations, we built Prime Sandboxes: a fully redesigned, high-performance execution layer that bypasses the Kubernetes control plane, delivers near–local-process latency through a direct Rust-to-pod execution path, achieves sub-10-second startup at massive concurrency, and scales to hundreds of isolated sandboxes per node.

Within verifiers, we overlap sandbox provisioning with first-turn model reasoning to completely hide the startup time before code execution is required.

For full details on how we built and optimized our sandboxes for training INTELLECT-3, see our technical report.

Compute Orchestration

We deployed 512 NVIDIA H200 GPUs across 64 interconnected nodes. The primary engineering challenge lies in maintaining determinism and synchronization across a distributed system prone to hardware failures.

• Provisioning: Infrastructure-as-Code via Ansible, automatic hardware discovery, and pre-run InfiniBand checks that isolate slow or faulty nodes.
• Orchestration: Slurm + Cgroup v2 ensures clean job teardown and prevents leftover processes from blocking GPU memory.
• Storage: Lustre for high-throughput training I/O, and NVMe-backed NFS for fast metadata and seamless SSH access.
• Observability: DCGM + Prometheus monitoring lets us catch errors early and drain unstable nodes before they impact training.

INTELLECT-3 Training Recipe

INTELLECT-3 was trained in two main stages: a supervised fine-tuning stage on top of the GLM-4.5-Air base model, and a large-scale RL stage. Both stages, including multiple ablations, were carried out on a 512-GPU H200 cluster over the course of two months.

We trained on a diverse and challenging mix of RL environments designed to enhance the reasoning and agentic capabilities of our model. All RL environments we use are publicly available on the Environments Hub. We include the following categories: Math, Code, Science, Logic, Deep Research, and Software Engineering

Standardized and validated implementations of all benchmarks are available on the Environments Hub. Full details on our training recipe can be found in our technical report.

Resources

We open-source INTELLECT-3, our training framework RL prime-rl, and all environments used for synthetic data generation, training, and evaluation.

• Technical Report: storage.googleapis.com/intellect-3-paper/INTELLECT_3_Technical_Report.pdf
• Model Weights: huggingface.co/PrimeIntellect/INTELLECT-3
• PRIME-RL: github.com/PrimeIntellect-ai/prime-rl
• Verifiers: github.com/PrimeIntellect-ai/verifiers
• Environments: hub.primeintellect.ai

Future Work

We’re looking forward to extending this work to:

• Scaling Agentic RL: For the INTELLECT-3 checkpoint we release, rewards and evaluations continue to rise, and training remains stable. We are continuing to train with an increased emphasis on agentic environments in our RL mixture, and we expect to observe additional gains across a wider range of tasks in a subsequent release.
• Richer RL Environments: The Environments Hub now has 500+ tasks across research, computer use, theorem proving, automation, and specialized domains. INTELLECT-3 used only a small fraction; the next step is scaling RL across a broader, higher-quality set of community environments.
• Long-Horizon Agents: We’re making long-horizon behavior trainable via RL by allowing the model manage its own context—cutting context, branching, and maintaining lightweight external memory—so it can learn end-to-end context handling. So, we’re also looking towards environments that reward long-horizon reasoning directly.

Chat with INTELLECT-3

Chat with the model at chat.primeintellect.ai or via our Inference API.
‍
Thank you to Parasail and Nebius for being inference providers of the model.

Towards Open Superintelligence

We believe in a future where every company can be an AI company.

Where we can have a flourishing ecosystem of startups and companies building their own models. Where we can democratize access and ownership in the upside of the Intelligence Era, rather than being dependent on a set of obscure models hidden behind the APIs of companies that explicitly want to win and own it all.

Prime Intellect is building the open superintelligence stack, putting the tools to train frontier models into your hands. INTELLECT-3 serves as an example that you don’t need to be from the big labs to train models that compete in the big leagues.

We’re excited to see what you build with INTELLECT-3.

‍